目录
前言
课题背景和意义
实现技术思路
一、DAFDC-RNN模型的构建
二、实验分析
实现效果图样例
最后
前言
📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。
🚀对毕设有任何疑问都可以问学长哦!
选题指导: https://blog.csdn.net/qq_37340229/article/details/128243277
大家好,这里是海浪学长毕设专题,本次分享的课题是
🎯基于深度学习的时间序列预测方法
课题背景和意义
时间序列是一种广泛存在于现实各领域之中的海量高维数据 , 时间序列预测是该领域的一个研究重
点 . 传统的时间序列预测方法仅仅从时间的维度对时间序列进行分析 , 忽略了外界影响因素对时间序列可能产生的影响. 针对传统时间序列预测方法存在的问题 , 提出一种基于深度学习的时间序列预测模型 DAFDC-RNN (dual-stage attention and full dimension convolution based recurrent neural network).为了解某种事物的发展规律,人们通常会以一定的采样频率对该事物的某项指标进行观测,这种按照时间先后顺序所产生的观测值集合就是时间序列. 对时间序列的历史观测值进行分析,并推测出未来时间节点上值的过程称为时间序列预测. 时间序列预测已经应用于众多领域之中,具有重要的现实意义. 例如,在生态环境领域,可通过对日降水量进行预测来指导农业生产;在医疗领域,可通过对疾病发病率进行预测来预防疾病传播;在经济领域,可通过对房价进行预测来稳定国民经济和维护社会稳定.
实现技术思路
一、DAFDC-RNN模型的构建
问题定义及符号表示
DAFDC-RNN 模型的输入有 1 至 T − 1 时刻输入特征组成的多变量时间序列X 和 1 至 T − 1 时刻被预 测特征组成的单变量时间序列Y . X = ( x 1 , x 2 , . . . , x t , . . . , x T − 1 ) = ( x 1 , x 2 , . . . , x k , . . . , x n ) T ∈ R n × ( T − 1) , Y = (y 1 , y 2 , . . . , y t , . . . , y T − 1 ) T ∈ R ( T − 1) × 1 , T 表示时间序列的步长 , n 表示输入特征的特征数量; x t ∈ R n × 1 , 表示 n 个特征在 t 时刻的特征值集合; x k ∈ R ( T − 1) × 1 , 表示 1 至 T − 1 时刻 , 由第 k 个特征组成的时间序列; y t ∈ R , 表示被预测特征在t 时刻的特征值.
DAFDC-RNN 模型的目标是预测出 T 时刻被预测特征的特征值y T , 即需要学习一个非线性关系 F , 使得F 满足如下公式 :

模型描述
DAFDC-RNN模型使用编码器-解码器结构,在编码器中引入目标注意力(target attention)机制和全 维度卷积(full dimension convolution, FDC)机制,在模型解码器中引入时间注意力(temporal attention) 机制.DAFDC-RNN模型的结构:
1) 目标注意力机制
某个特定时刻被预测特征的特征值是所有输入特征综合作用的结果, 即目标特征与输入特征之间具
有一定的相关性 , 并且通常情况下不同的输入特征与被预测特征之间的相关性大小也是不同的,
为了量化 t 时刻模型输入中的第 k 个特征与被预测特征的相关性大小, 首先为第 k 个特征定义上下文
向量 context k t , 有:
为了将 context k t 与被预测特征组成的时间序列 Y 之间建立关联 , 引入注意力机制中的点积评分函 数:
2) 全维度卷积机制
针对多变量时间序列在特定时刻的特征值集合, 提出一种全维度卷积机制 , 该机制不仅能够克服传统CNN 模型需要手动设置大量参数的弊端, 同时可以充分学习输入特征之间的相关性 .
FDC 中使用 Concat 层代替传统 CNN 模型中的全连接层, 不仅仅是为了避免手动设置神经元数量等参
数 , 更是为了防止全连接层破坏输入特征之间的相关性.
下面对卷积层、池化层和Concat层中关键步骤的公式进行说明.根据t时刻FDC的输入 ext 和卷积层中第p个卷积核,可以得到t时刻卷积层第p个特征图的第i(i = 1, 2, . . . , n − p)个值为:

3)时间注意力机制
随着输入序列长度的不断增加, 编码器-解码器结构的性能会迅速下降. 为了解决这一问题, DAFDC-RNN模型在解码器中引入temporal attention机制,自适应地选择相关的编码器隐藏层状态.在任意时刻t,解码器会利用temporal attention计算出一个上下文向量βt ,有
4)模型输出
通过感知器将解码器的上下文向量βt和被预测特征的特征值yt 建立关联,可以得到t时刻解码器隐 藏层的输入为。

算法的工作过程
首先对输入的每个时间步 x t 引入目标注意力机制, 计算当前时间步的所有输入特征与被预测特征的相关性, 为不同的输入特征分配相应的权重 a k t , 从而得到t 时间步目标注意力的输出˜x t .
算法效率分析
在目标注意力机制每个时间步长 , 计算每个特征上下文向量的浮点运算次数(FLOPs) 为 ( T − 1)(2 m + 1), 点积评分函数的 FLOPs 为 ( T − 1) . 因此目标注意力机制的T ( n ) = ( T − 1) n (( T − 1)(2 m +1)+( T − 1)) ,
即 T ( n ) = O (( T − 1) 2 ) . 在全维度卷积机制每个时间步长, 卷积计算输出的 FLOPs 为 n∑ i =1 i ( n − i + 1) , 因此全维度卷积机制的T ( n ) = ( T − 1) n∑ i =1 i ( n − i + 1), 即T ( n ) = O ( n 2 ) .
二、实验分析
模型超参数
DAFDC-RNN模型中共有3个超参数,分别是时间步长T、编码器隐藏单元大小和解码器隐藏单元大小.给定T 的取值集合为{4, 6, 8, 10, 12, 14}, H 的取值集合为{16, 32, 64, 128, 256},理论上单个数据集需 要进行30(6 × 5)次实验才可以确定T 和H 的最佳组合. 本研究对超参数实验过程进行简化:当对T 的取值进行实验时,固定H 的值为64;当对H 的取值进行实验时,固定T 的值为10. 最终单个数据集需要进行11 (6 + 5)次实验就可以确定T 和H 的最佳组合。

对比实验
为了进一步验证 DAFDC-RNN 模型的预测能力 , 选用以下3 种对比模型与 DAFDC-RNN 模型的预测效果进行对比: 1) ARIMA; 2) Encoder-Decoder(也称为 Seq2seq); 3) DA-RNN. 需要注意的是,Encoder-Decoder 和 DA-RNN 模型与DAFDC-RNN 模型一样有时间步长 T 和隐藏单元大小H 两个超参数 . 为了保证实验的公平性 , 同样需要确定Encoder-Decoder 和 DA-RNN 模型两个对比模型的最佳超参数组合。
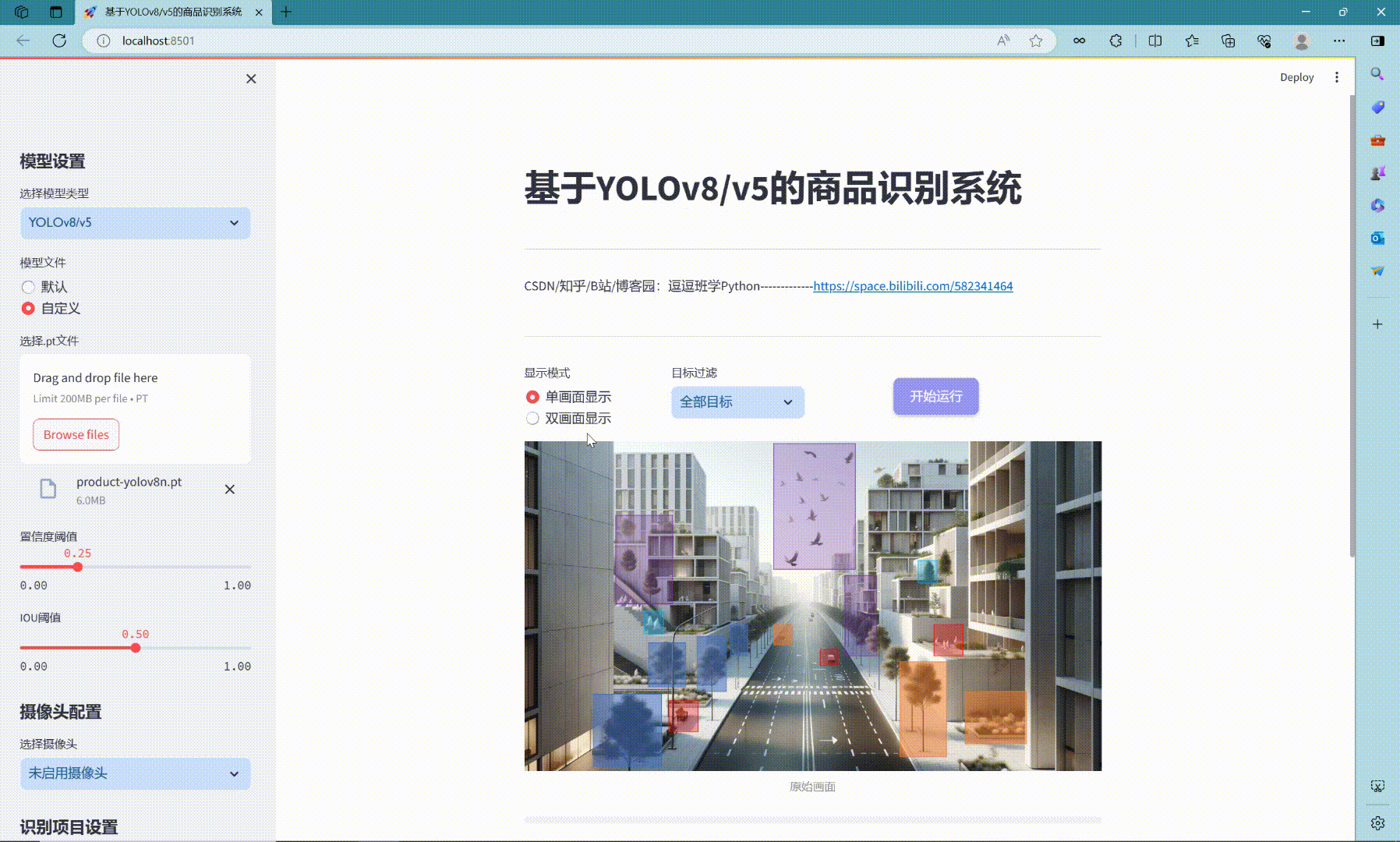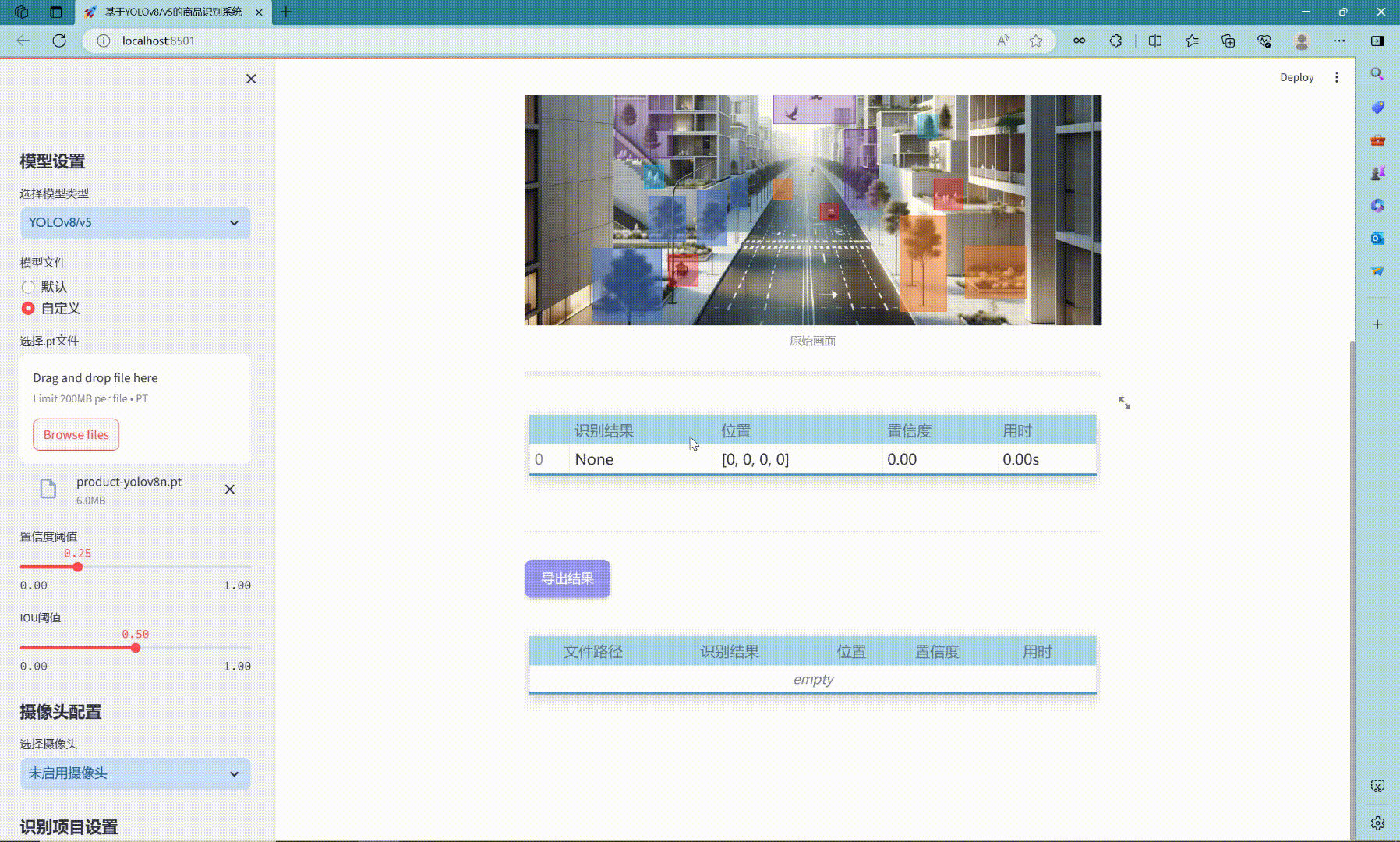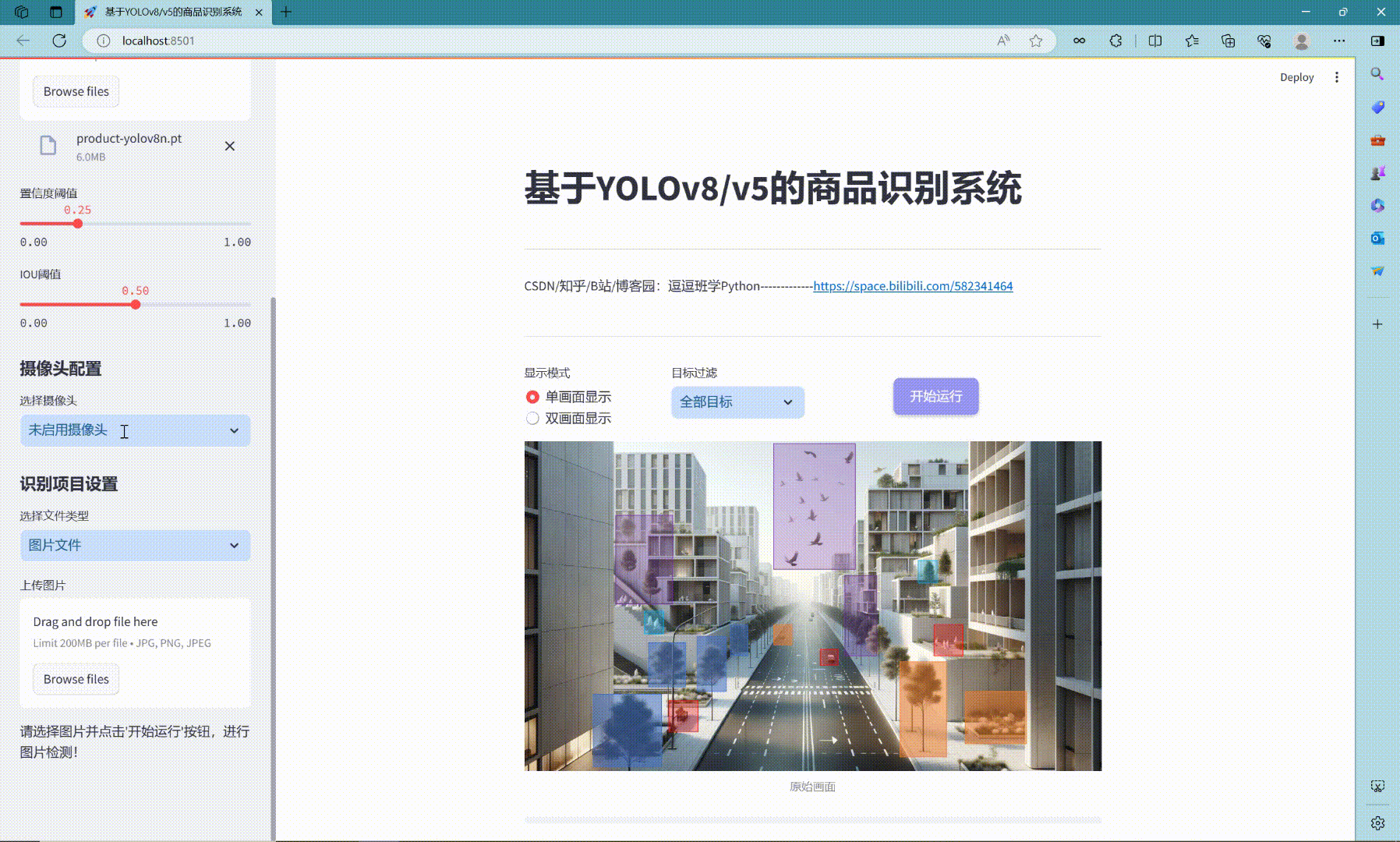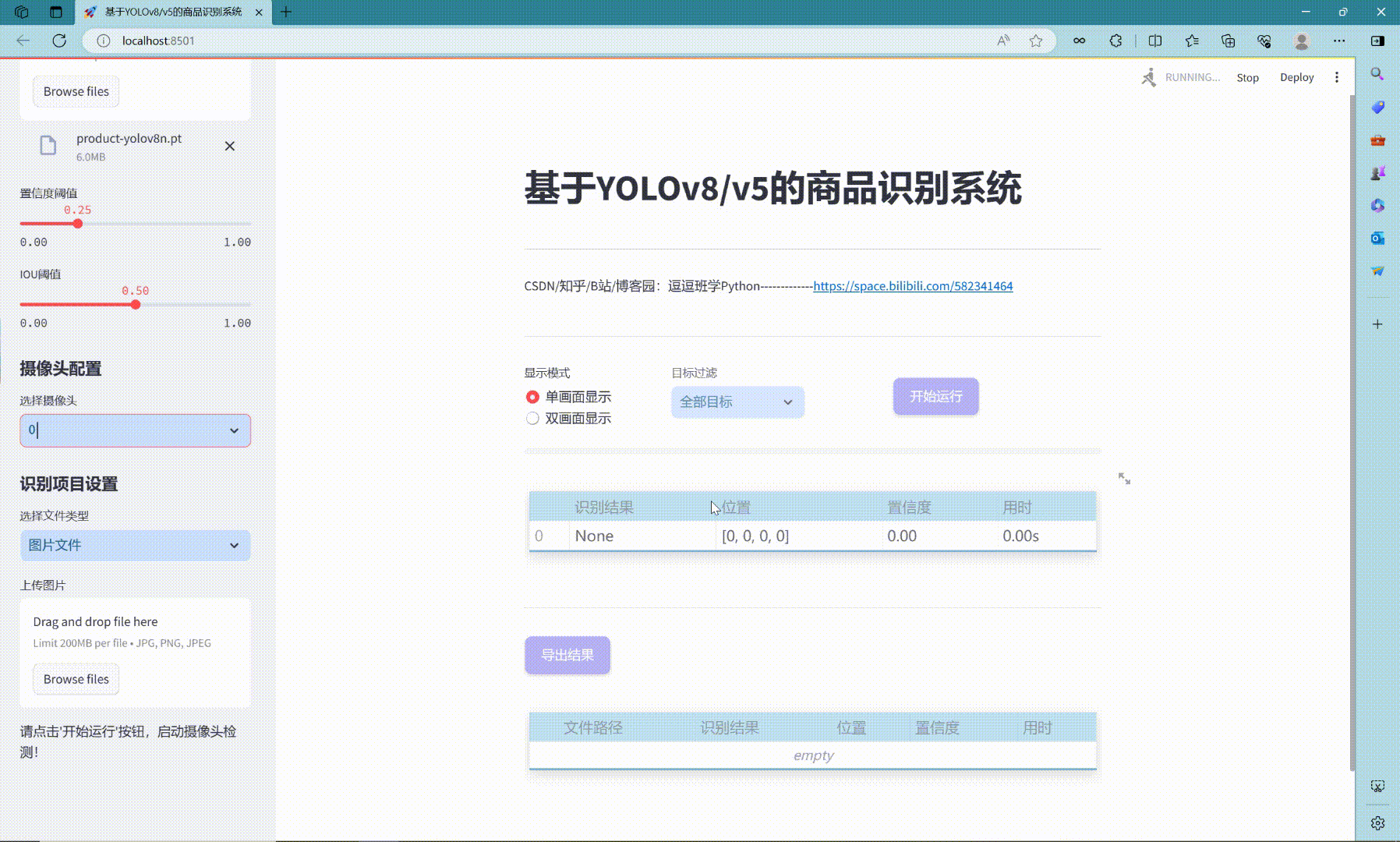
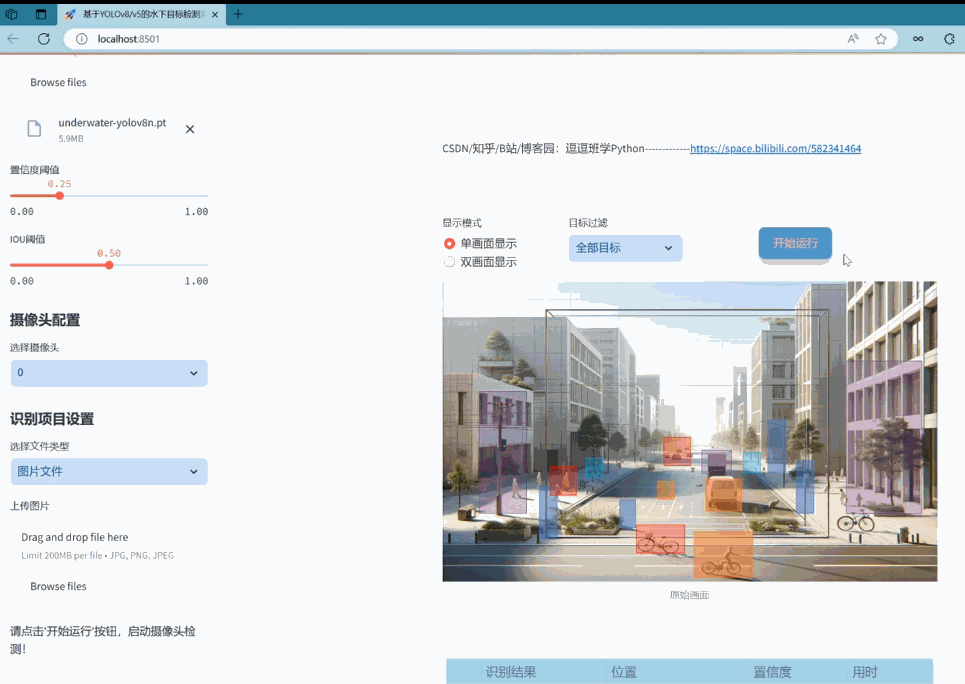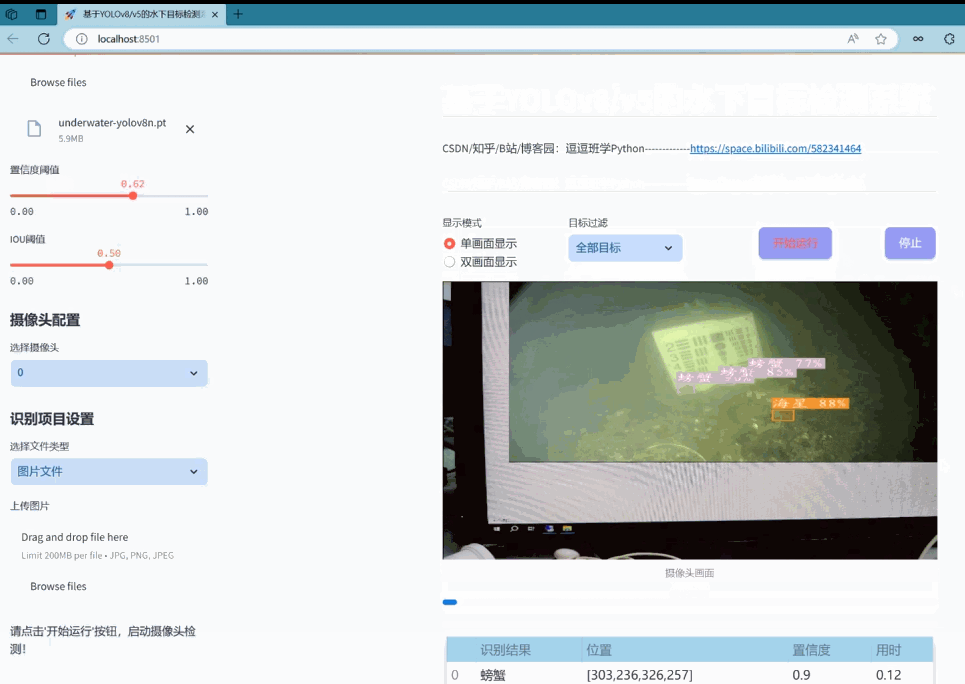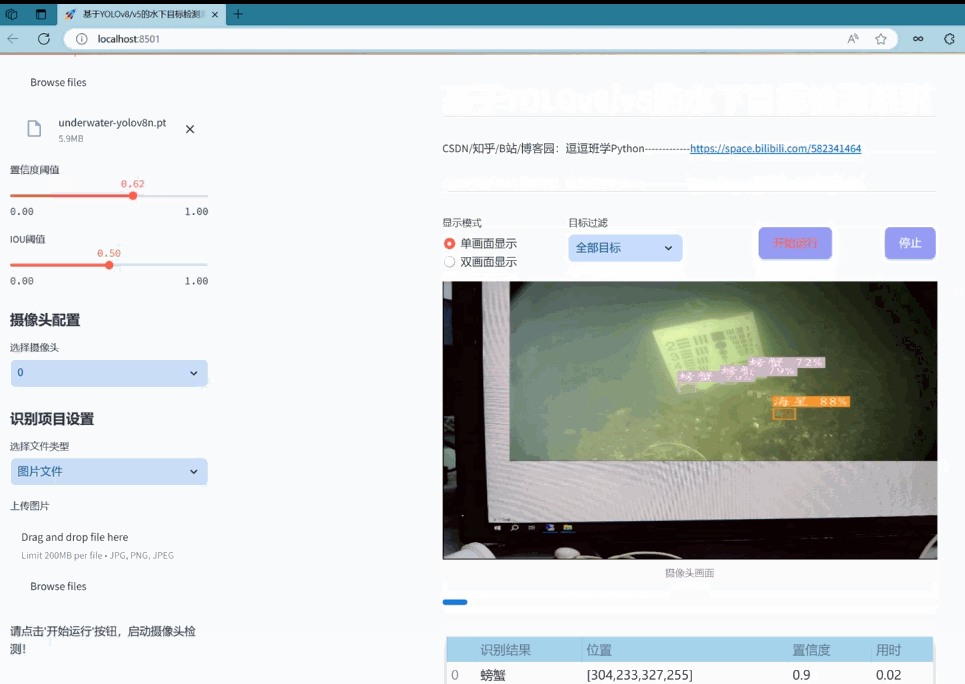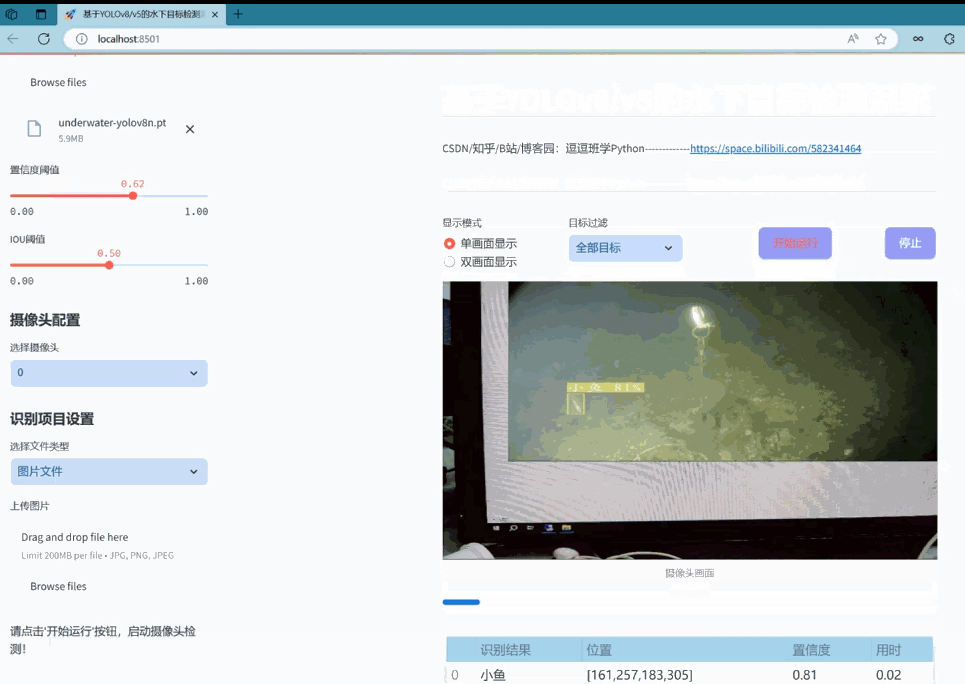
实现效果图样例
利用eviews做ARMA时间序列分析:


我是海浪学长,创作不易,欢迎点赞、关注、收藏、留言。
毕设帮助,疑难解答,欢迎打扰!
最后
![]()

![]()




![]()




 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)