1、背景

设计高性能的深度神经网络是一项具有挑战性的工作，需要设计人员拥有丰富的专业知识以及调参经验。Neural Architecture Search（NAS）降低了从业人员设计训练网络的难度。NAS主要涉及模型结构的生成和精度预测两部分。常见的生成算法包括均匀采样，进化算法和强化学习。精度预测包括暴力计算，训练预测器预测和单次超网络训练预测（one-shot）。 当前构建高质量预测器的主要挑战是庞大的计算代价。暴力计算和训练预测器的方法均需要训练可观数量的网络。one-shot可以通过权重共享减少训练代价，但仍需要训练一个超大网络，并且有研究发现，基于超大网络的方式得到的模型精度与模型实际精度不一致。 本文介绍一篇使用zero-shot方法评估模型的论文ZenNAS[1]。论文中利用深度神经网络的表达能力与模型精度呈正相关的关系，设计了一种测量网络表达能力的方法Zen-Score。论文中的方法受到了近期深度学习研究的启发，在相同数量的神经元下，深度模型比浅层模型有更高的表达能力。根据统计学习理论中的偏差-方差平衡内容，增加深度网络的表达能力意味着更小的偏差误差。当训练集足够大时，方差误差将接近0。这意味着表达能力更强的网络可以减少由偏差误差决定的泛化误差。这些理论结果与大规模深度学习实践一致。 论文使用Zen-Score搜索出的深度神经网络，在ImageNet数据集上获得最高83.6%的精度，同时模型的推理时间也被约束在特定范围内。

2、模型表达能力

2.1 符号说明

这里先对常用的符号进行说明，对于L层网络可以用函数表示成 ƒ：ℝ^m0→ℝ^mL，其中m₀是输入维度，m_L是输出维度。x₀ ϵ ℝ^m0表示输入图片。相应的第t层的输出特征图表示为x_t。第t层有m_t-1个输入通道和m_t个输出通道。卷积核为。图片分辨率H✖W。小批量为B，均值μ方差σ²的高斯分布表示为N(μ,σ)。

在深度学习的理论研究中，广泛使用的是普通的卷积神经网络（vanilla convolutional neural network，VCNN）。普通网络的主干由多个卷积层堆叠而成，每层包括一个卷积操作，紧跟一个RELU激活函数。主干中的其他所有成分如残差连接（residual link）、批量归一化（Batch Normalization）等被移除。主干之后是全局平均池化层（GAP），再跟一个全连接层。最后使用soft-max运算将网络输出转换为标签预测。因为网络主干部分包含大部分所需信息，因此仅使用主干部分测量网络的表达能力。

论文中也解释了去掉网络附加结构后，不会显著影响网络的表达能力。如BN层可以使用卷积核融合，将其并入到卷积核中。自注意力机制是特征图的线性组合，得到的结果仍在同一子空间内。对于非RELU激活函数，可以将其替换为RELU。上面这些调整对大多数非VCNN网络适用。实际上几乎所有单分支前馈网络均可使用前面的操作转换为普通网络。

2.2表达能力代理Φ-Score

论文研究了最近有关深度网络表达能力的理论研究，发现这些研究存在一些共同点，就是对于一个普通的网络可以在激活模式上分解成分段的线性函数[2]，见引理1。

Lemma 1. 网络第t层的激活模式表示为Α_t(x)。那么对于任意普通网络f(·), 

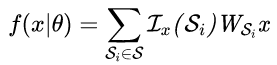
其中S_i是由{Α₁(x),Α₂(x),...,Α_Լ(x)} 决定的凸多面体；S是R^m0中的有限凸多面体集合；如果xϵS_i，则Լx(S_i)=1，否则为0；W_Si是R^mL×m0大小的系数矩阵。 

根据推论1知道，任何普通网络是由凸多面体S={S₁,S₂,...,S_|S|}分割成的分段线性函数的集合，其中|S|为线性区域的数量。在几个研究[3][4][5]中均使用线性区域的数量|S|表示表达能力。但是这种方法存在两个限制。一是对于大型网络，计算|S|是不可行的，二是没有考虑到每个W_Si的表达能力。第一个限制是由于对于大型网络，线性区域的数量是呈指数增长的。对于第二个限制的说明，考虑线性分类器的高斯复杂度，见引理2。 

Lemma 2. 对于线性函数类，它的高斯复杂度的上界由Ϭ(G)确定

推论2说明高斯复杂度衡量的线性函数的表达能力是由参数矩阵W的F-范数控制的。从引理1和引理2出发，可以得到测量网络表达能力的定义：

Definition 1 (VCNN的Φ-score). 普通网络f(·)的高斯复杂度的期望定义为 

定义1中使用高斯复杂度的期望测量网络的表达能力或Φ-score。因为VCNN网络是线性函数的组合，很自然地会通过计算每个线性区域内线性函数的高斯复杂度的平均值表示网络的表达能力。从某些先验分布随机采样x和θ，然后对||W_Si||_F取平均。这等价于计算f对x的梯度范式的期望。这样就得到了计算模型Φ-score的公式。 

接下来，论文说明了直接计算深度网络的Φ-score，会出现数值溢出的问题。一般梯度爆炸问题可以通过向网络中加入BN层来解决，但这使得Φ-score自动缩放，很难去比较不同网络的Φ-score。这种现象在深度学习的复杂度分析中称为尺度敏感问题。论文中为了解决该问题，使用BN层的方差统计量的乘积对Φ-score重新缩放多次，新的score称为Zen-Score。为了区分原始的Φ-score，论文证明了Zen-Score是尺度不敏感的。 

图1中对比了Φ-score和Zen-Score对于不同深度和宽度网络的效果，从图(a)(b)(d)(e)中可以看到前面提到的Φ-score问题，使用提出的Zen-Score方法，可以正确显示出网络深度、宽度与复杂度的关系。 

图1. Φ-score和Zen-Score对不同深度和宽度网络的效果 

2.3 Zen-Score

Zen-Score是为解决Φ-score的尺度问题所提出的，因为Zen-Score是在Φ-score的基础上进行了缩放，为了证明Zen-Score的有效性，只需要证明Zen-Score乘以缩放系数后可以近似Φ-score。即只需要证明下面定理1成立。

Theorem 1. 假定是一个没有BN层的L层的原始网络。f(x₀)=x_L是含BN层的相似网络。对于常数，当足够大时，概率至少为1-δ，有：

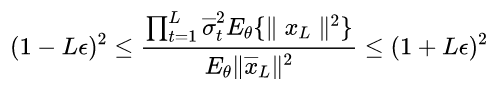
其中 。

定理1说明为了计算，只需要计算||f(·)||，然后使用进行缩放，近似误差限制在L_ϵ。定理1的证明借助了Bernstein’s inequality。具体的证明细节可以阅读论文附录部分。 

Zen-Score的计算过程如Algorithm 1所示，首先对网络进行预处理，移除网络中所有的残差连接，然后随机采样获得输入矢量，以及向输入矢量添加高斯噪声扰动。特征图的扰动表示为，该步替代了对x求解梯度。为了得到Zen-Score，缩放系数是BN层每个通道方差的均值。最后，计算出和的log-sum。 

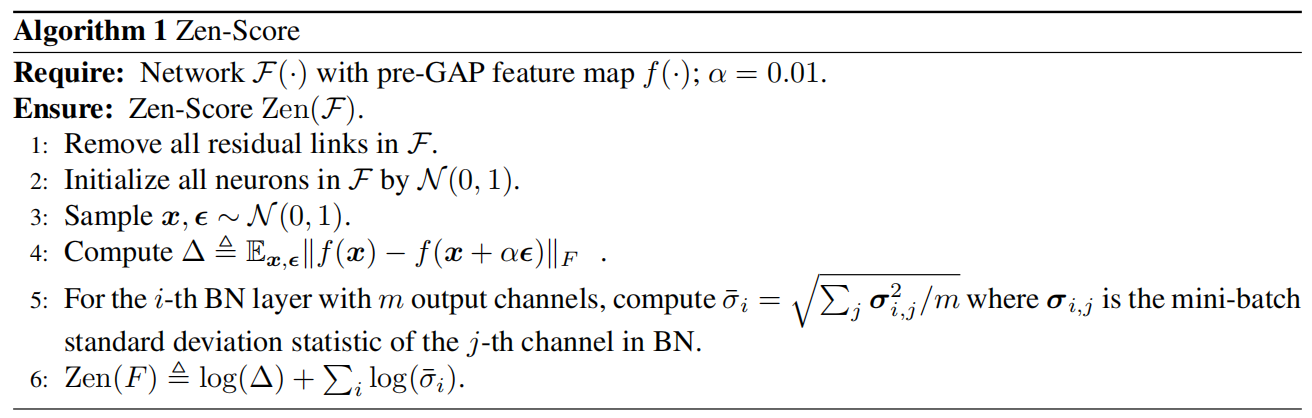
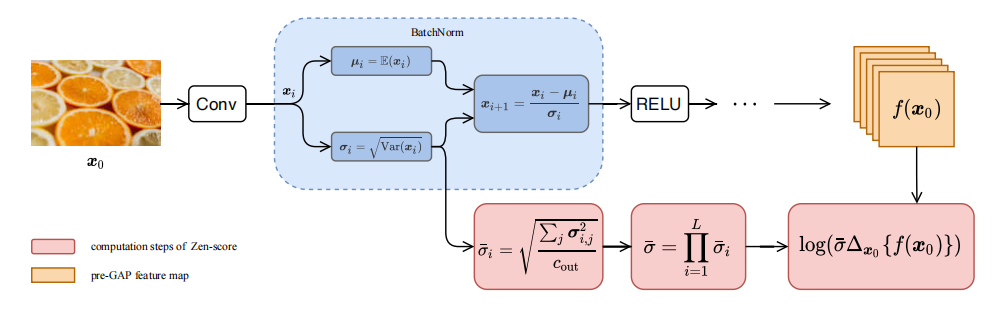
图2. Zen-Score 计算图 

图2为Zen-Score计算图，x₀是小批量的输入图片，对于每一个BN层，提取小批量的方差（deviation）σ_i，是全局池化层之前的特征图 f(x₀)对x₀的微分，两者相乘再取log得到模型的Score。 

2.4 ZenNAS算法

为了使目标网络的score最大化，设计了Zen-NAS算法。算法中使用进化算法产生网络结构并进行选择。具体算法见Algorithm2，首先随机生成M个满足budget B的网络结构F₀，这些初始结构构成了初始群体P，每次迭代中，随机从群体P中选择F_t个体进行变异（见Algorithm3），获得变异个体，如果满足budget并且网络层数小于L，则计算网络的Zen-Score，并将其添加到群体中，为了维持群体数量的稳定，当群体数量大于N时，将最小Score的个体剔除出群体中，经过T次迭代后，返回群体中最高Score对应的个体F*。

在对网络F_t进行突变时，从搜索空间S中随机选择一个block，并在F_t中随机选择一个block进行替换，并且对block的参数如卷积核大小，通道宽度和深度在一定范围内进行改变。最后，返回变异结构。 

使用论文提供的方法，可以快速的搜索出高精度的网络，如图3所示，Zen-NAS在ImageNet上可以得到最高精度为83.6%，仅需0.5GPU天。论文中统计的搜索时间为模型score的耗时，整个搜索过程的时间会稍长。 

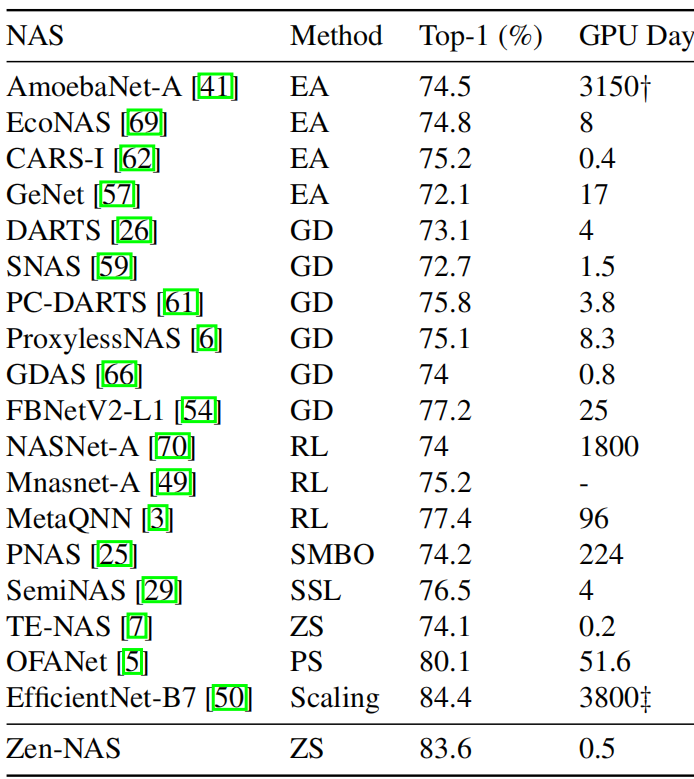
图3. 不同NAS方法搜索的网络在ImageNet上的精度和耗时

另外对于模型训练，根据开源代码中提供的蒸馏方法，训练后的模型精度可以提升3%以上。我们测试过仅使用数据增强方法和传统蒸馏的模型训练，最终的模型精度无法达到与论文相同的结果，训练的模型精度要低3%以上。相比原始蒸馏方法，论文中增加了特征图loss，说明通过增加特征图损失，可以有效de提供模型蒸馏的效果。 

参考文献

[1] Lin, Ming, et al. "Zen-NAS: A Zero-Shot NAS for High-Performance Image Recognition." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021. 

[2] Guido Montufar, Razvan Pascanu, Kyunghyun Cho, and Yoshua Bengio. On the Number of Linear Regions of Deep Neural Networks. In NIPS, 2014. 

[3] Boris Hanin and David Rolnick. Complexity of Linear Regions in Deep Networks. In ICML, 2019. 

[4] Thiago Serra, Christian Tjandraatmadja, and Srikumar Ramalingam. Bounding and Counting Linear Regions of Deep Neural Networks. In ICML, 2018. 

[5] Xiao Zhang and Dongrui Wu. Empirical Studies on the Properties of Linear Regions in Deep Neural Networks. In ICLR, 2019.