算子融合也称符算融合，作为面向DL模型推理的一种关键图优化技术，通过减少计算过程中的访存次数达到提升模型推理性能的目的，该技术在不同时期、不同框架下的落地方式各不相同。本文将首先带大家回顾算子融合技术的发展历程，并浅析其中颇有代表性的Apollo方案。

1.算子融合技术的发展历程

大约16年前后，业界对于推理应用的性能诉求还不普遍，对于有性能需求的场景，最常见的做法是利用设备供应商提供的API加速计算图中的部分计算密集型（Compute-bound，以下称CB）算子，如Conv、Dense等。这一时期，用户自定义的算子融合多半是相邻访存密集型（Memory-bound,以下称MB）算子的融合；而典型的CB+MB形式的融合（例如Conv+ReLU）则受限于供应商API的支持程度。

随着AI模型在各领域的发展、成熟和落地，模型推理在具体设备上的性能变得越发重要，17年到18年，业界出现了大量面向DL模型推理的计算框架，算子融合技术在不同框架上呈现出两种典型的发展路线：

1. 遍历路线：针对特定设备，枚举实现典型的CB+MB形式的融合算子，如Conv+ReLU/Conv+BN+ReLU/Dense+ReLU/Conv+Sum等等，Intel的oneDNN以及国内很多大厂的推理框架走的都是这个路线。
2. 规则路线：基于规则实现算子融合，以TVM为例，其将所有算子分为Opaque/Injective/Reduction/Complex-out四类，并设定融合规则形如Complex-out+Injective/Injective+Injective/Injective+Reduction等，以此实现所有符合规则的子图融合。

两种路线相比各有优劣：

1. 对于业务范围、应用设备十分明确的场景，遍历路线更适合在短期内迅速提升模型的执行性能。假设某公司的业务是在ARM设备上做Resnet模型的推理，那么提升模型推理性能的最直接手段必然是实现不同Workload的Conv+BN+ReLU子图在ARM设备上的最优流水排布、数据并行方式、循环拆分合并等。同时，这一路线的缺点也十分明显：没有泛化性，如果部署设备、模型等要素发生变化，之前的工作对当前工作没有任何帮助。
2. 规则路线显然具备更佳的应用泛化性，但融合后子图的执行性能却不一定足够好：以Conv为例，假设在TVM中某个Conv算子在X86设备上按照调度方案A被拆分为9层循环，那么后继的ReLU算子应该在哪层循环计算才是最优？最优位置是否和Conv算子的Workload相关？如果有新类型的CB算子，以上问题的答案是什么？想要解决以上问题，在当前的TVM框架下可以通过对特定子图注册不同的compute-schedule模板，配合AutoTVM搜索给出近似最优解，但schedule的改动和调整仍然需要人工参与。

以上提到的算子融合解决的是典型的“内存墙”问题，即减少缓存和内存间数据搬运量以提升计算性能。除此以外，还有一些算子融合技术解决的是“并行墙”问题，即如何保证计算图执行非CB部分的子图时也能充分利用设备的计算资源，这方面典型的工作是TASO和RAMMER，通过将计算过程中互不依赖的低计算量子图打包为一个kernel并行计算以提升资源利用率。

2. Mindspore的算子融合方案Apollo

Apollo是Mindspore框架的图算融合团队提出的多层规约算子融合方案，其分为两个主要阶段：

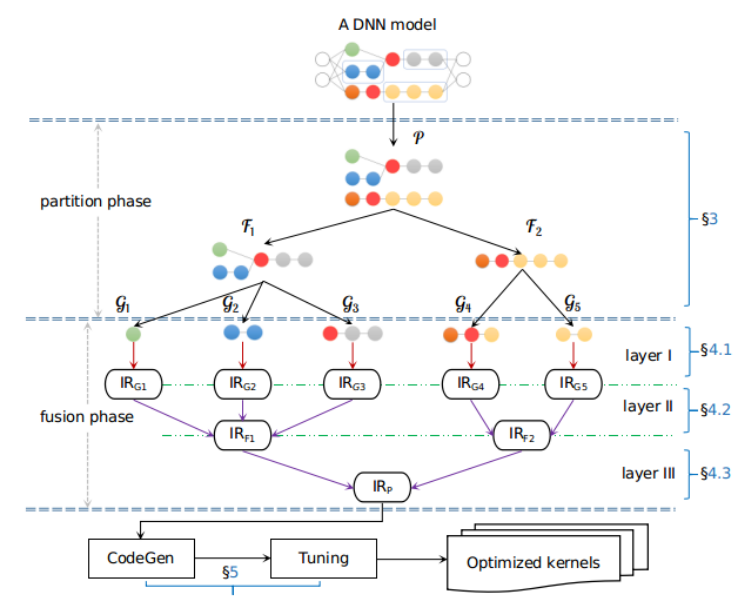
1. 首先是图划分阶段，提取DNN模型的所有subgraph，并将subgraphs根据预定的规则重新分解并聚合成更合理的micrograph，这一步的目的是让所有可能后续做融合的子图聚合为micrograph，为后续所有融合工作划定范围
2. 再就是基于以上拆分得到的micrographs做了bottom-up的重新融合，分为三步：a. 基于Polyhedral启发算法做loop fusion，这一阶段将诸如Dense+ReLU、Conv+ReLU形式的子图做循环级别的融合 b. 继续融合优化非CB算子，此步骤参考了阿里的AStitch工作，通过对计算图算子级别依赖和元素级别依赖的分析，将MB算子尽可能融合 c. 基于以上的融合结果，做了类似TASO和RAMMER的工作，识别无计算依赖的算子做并行计算

2.1 图划分的具体步骤

图划分是Apollo方案非常重要的一步，比如对于CB算子和injective算子的融合，图划分起的作用是将可以融合的计算尽可能分到一个group里，后续的Polyhedral融合就是在这个group里决定融合的具体循环位置，该步骤可以分为以下三步：

1. 将所有合适做融合的算子提取出来，这里的“合适”指除了自定义算子、计算量超复杂的算子以及控制流算子之外的所有算子

2. 分解compound算子，比如对于以下例子中的LogSoftMax算子，该算子是由reduce和substract算子组合的，这一步要把这种算子拆分，为后面的merge提供更多可能性

        3.primitive算子聚合，这一步类似于TVM的规则定义和应用，Apollo把算子定义为element-wise/broadcast/reduce/opaque四种算子，根据以下rules做的算子聚合分组：

2.2 图融合的具体步骤

Apollo采用了bottom-up多层规约融合的方法实现的融合，依次解决了buffer/loop级别融合、“内存墙”突破融合以及“并行墙”突破融合：

  1.  loop级别的融合采用Polyhedral启发式算法，实现循环合并工作，例如下面例子中实现的add+pooling的融合：

   2.“内存墙”突破参考的是阿里的AStitch工作，“内存墙”问题体现比较明显的一个例子是BERT这种transformer模型的图融合场景：BERT模型中的CB算子是矩阵乘，相邻的矩阵乘算子间会有数个MB算子，对这些MB算子做融合会遇到两难问题，即不做会有大量kernel的启动开销影响性能；做了会因为broadcast算子和后续计算的自动合并导致硬件计算资源被空耗（重复计算）。因此阿里提出了AStitch工作，对MB算子图做了op依赖和element依赖分析，可以避免一些MB算子融合带来的重复计算问题，Apollo复用了这个工作

  3. 并行墙”突破主要是将无依赖计算合并到一起做并行计算，这里的关键在于如何在避免组合爆炸的前提下对可以并行的子图分组，Apollo的做法是基于经验总结了以下几种常见的模式：

2.3 技术效果

MindSpore 1.3版本发布Bert GPU网络，Apollo方案的应用实现了相对XLA 3.1~3.6倍的性能加速。

3. 观点总结

1. 受限于通用计算设备的算力增长瓶颈，算子融合技术仍然是提升模型推理在这类设备上推理性能的重要手段
2. 解决“并行墙”问题的算子融合技术相对独立，适合大部分框架应用和借鉴
3. 面向“内存墙”的算子融合技术，Apollo的方案的一个重要基础是基于Polyhedral的自动循环优化，这对于很多小伙伴来说是个门槛
4. Polyhedral不一定是算子自动循环优化的最优解法，基于此的CB+MB融合也不是唯一方案，例如小节1提到的“半自动”搜索方法也能在同样的任务下获得相似的性能，实现难度也更低