通过训练，神经网络就可以使用更低精度的数据格式（包括浮点、定点和整数）进行推理。低精度数据格式提供了几个性能优势：

  • 许多处理器通过 low-bit 格式提供更高吞吐量的数学管道，这可以加快计算密集型的运算，如卷积和矩阵乘法；
  • 低精度的数据格式可以减少了内存带宽压力，提高了带宽有限计算的性能；
  • 低精度的数据格式可以降低内存大小的需求，这可以提高缓存利用率以及内存系统操作的其他方面。

本文主要研究神经网络模型推理的整数量化，其中网络模型在推理时使用整数权重和激活。表 1 列出了 NVIDIA Turing GPU 体系结构中各种数据类型相对的张量运算吞吐量和带宽减少倍数。与 FP32 中的相同操作相比，在 INT8 类型上执行的数学密集型张量运算的速度可以提高 16 倍。与 FP32 数据类型相比，受内存限制的运算，INT8 可以提高 4 倍的速度，因为它的位数更小。其他处理器，如 TPU，带有 VNNI 指令的英特尔 CPU 和许多新兴的加速器设计都为 INT8 操作提供了显著的加速。

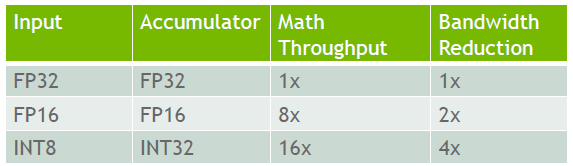
表 1 NVIDIA Turing GPU 架构中张量运算的低精度数据类型的优势

1. 量化基础

均匀量化可分为两步：

  • 首先，选择要量化的实数的范围，限制在该范围之外的值；
  • 其次，将实值映射到可由量化表示的相应位宽的整数（将每个映射的实值四舍五入到最接近的整数值）。

在预先训练的浮点神经网络中启用整数运算需要两个基本操作：

  • 将实数转换为量化的整数表示（例如从 FP32 到 INT8）；
  • 将数字从量化的整数表示转换为实数（例如从 INT32 转换为 FP16）。

1.1 映射范围

 [β,α]为选择用于量化的可表示实值的范围， b为有符号整数表示的位宽。均匀量化将输入值 xϵ[β,α] 转换为 [-2b-1,2b-1-1] 整数范围内，其中超出范围的输入被截断到最近边界值。由于我们只考虑均匀变换，变换函数只有两种选择：f(x)=sx+z 及其特殊情形 f(x)=sx，其中 x,s,zϵ ℝ。

1.1.1 非对称量化

非对称量化映射实值x ϵ ℝ  到 一个b-bit 有符号整数 xq ϵ {-2b-1,-2b-1+1,...,2b-1-1}。公式 (1) 和 (2) 定义了非对称变换函数：

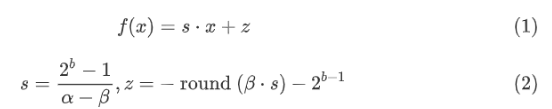
 其中s  是缩放因子，z 是零点，即实值零映射到的整数值。在 INT8 的情况下， 和 。 四舍五入为整数值，因此实数零可精确表示为整数。因此，需要对实际可表示范围  [β,α] 进行轻微调整。

公式 (3) 和 (4) 定义了量化运算：

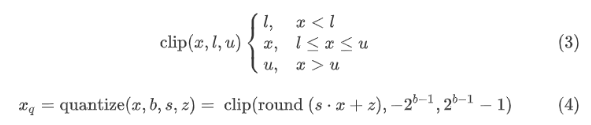
其中  round()四舍五入到最接近的整数。图 1a 显示了实值到具有非对称量化的 INT8 表示的映射。其中， s是可表示的整数与所选实数范围的比值。 

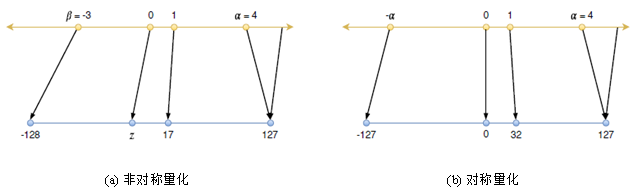
图1 实值到 INT8 的量化映射

公式 (5) 显示相应的去量化函数，该函数计算原始实数值输入的近似值。

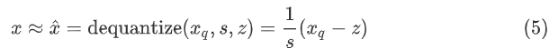
1.1.2 对称量化

对称量化仅通过缩放变换执行量化范围映射，输入范围和整数范围都是对称的。对于 INT8，使用整数范围 [−127, 127]，选择不使用值 -128 以支持对称。对于 INT8 量化，丢失 256 个可表示值中的一个是无关紧要。但对于较低的位宽整数量化，其可表示值和对称性之间的权衡应该重新评估。

图1b 说明了通过对称量化将实数值映射到 INT8。公式 (6) 和公式 (7) 定义了一个实值 x 的量化缩放因子，它具有一个选定的可表示范围 [α,α] ，产生一个 b-bit 整数值xq 。

公式 (8) 表示对称量化的相应去量化操作。

1.1.3 TensorRT 的 INT8 量化方式

对称量化最简单的线性映射的方式如图 2 所示。简单的将一个 tensor 中的-|max|  和 |max| FP32 类型的值映射为 -127 和 127 ，中间值按照线性关系进行映射，称这种映射关系为不饱和的。实验表明，这种映射会导致较大的精度损失。

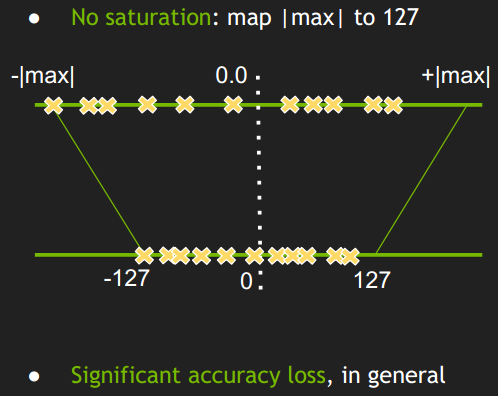
图2 对称不饱和映射 

因此，TensorRT 的 INT8 量化采用对称饱和线性映射的量化方式，如图 3 所示。饱和线性映射方式不是将 ±|max| 映射为 ±127，而是存在一个阈值|T|  ，将 ±|T|映射为 ±127，显然这里|T|<|max| 。超出阈值 |T| 外的直接映射为阈值±127 。比如上图中的三个红色点，直接映射为 -127。称这种映射关系为饱和的。只要阈值选取得当，就能将分布散乱的较大的激活值舍弃掉，也就有可能减少精度的损失。 

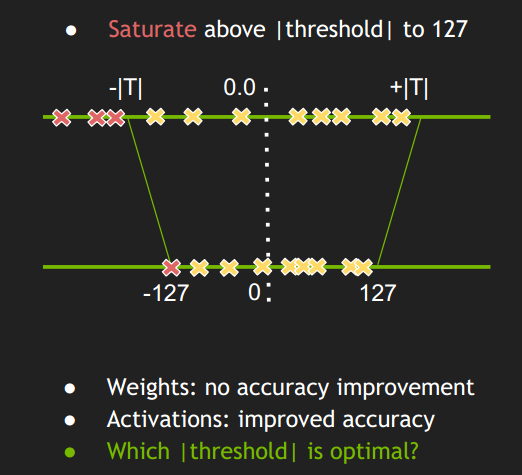
图3 对称饱和映射

那么下一个问题是阈值 T 的最佳值是多少？不同的数据类型表示不同的分布。对于使用 FP32 张量的原始模型，FP32 分布中表现得最好。但是，我们想用不同的分布（INT8）来表示它们，这不是最好的分布。我们想看看这些分布有多么不同，并希望将他们的差异最小化。TensorRT 使用 KL 散度 (Kullback–Leibler divergence，简称 KLD) 来度量两个分布的差异并将其最小化来寻找最佳的阈值 T。考虑两个分布 P（FP32）、Q（INT8）KL散度计算如公式 (9) 所示： 

 P，Q 分别称为referencedistribution   和  quantizedistribution。实际上这里也说明了每一层的 tensor 的|T|  值都是不一样的。确定每一层的|T|  值的过程称为校准 (Calibration) 。

1.2 Tensor 量化粒度

在 Tensor 元素之间共享量化参数有多种选择，我们将此选择称为量化粒度。在最粗粒度 per-tensor 上，tensor 中的所有元素共享相同的量化参数。最细的粒度将具有每个元素的单独量化参数。中间粒度在不同维度的张量上重用参数，如对于二维矩阵，每行或每列重用参数；对于三维（类似图像的）张量，每通道重用参数。

在选择粒度时，我们将考虑两个因素：对模型精度和计算成本的影响。为了理解计算成本，我们通过矩阵乘法来说明。考虑一个线性（完全连接）层执行矩阵乘法 Y=XW，其中  是输入激活张量， 是权重张量， 是输出张量。实值矩阵乘法  Y=XW的结果可以用量化张量近似  和 ，首先对它们进行去量化，然后执行矩阵乘法。考虑在最细粒度，每个元素量化的 tensor，采用对称量化：

 

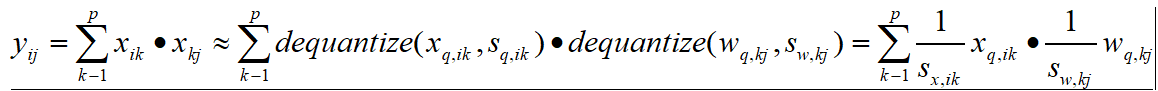
为了使用整数矩阵乘法，缩放因子必须从公式 (10) 右边的和中分离出来，因为公式 (10) 的缩放因子必须与  k无关： 

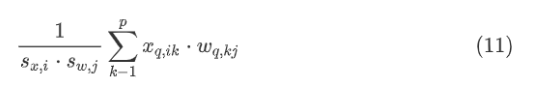
因此，只要量化粒度对于激活是 per-row 或 per-tensor，对于权重是 per-column 或 per-tensor，整数矩阵乘法就是可能的。对于激活，出于性能原因，仅 per-tensor 量化是可行的。在上述公式中，不同的行属于不同的批实例或序列中的项，行计数在推断时间可以变化。这样可以避免离线计算每行缩放因子（这对于小批处理中的不同实例没有意义），而在线确定它们会增加计算开销，在某些情况下会导致较差的精度。

为获得最佳性能，激活应使用 per-tensor 量化粒度。对于Y=XW  形式的线性层，权重应以 per-tenosr 或 per-column 粒度进行量化。卷积中 per-column 对应的粒度是 per-kernel，或等价于 per-output-channel（论文中通常称其为 "per-channel" 权重量化），因为每个卷积核产生一个单独的输出通道。

1.3 校准 (Calibration)

校准是为模型权重和激活选择 α 和 β 的过程。为了简单起见，我们描述了对称范围的校准，如对称量化所需。在本文中，我们考虑三种校准方法：

  • 最大值：使用校准期间看到的最大绝对值；
  • 熵：使用 KL 散度来最小化原始浮点值和量化比特表示的值之间的信息损失。这是 TensorRT 使用的方法。
  • 百分位：将范围设置为校准期间看到的绝对值分布的百分位。例如，99% 校准将截取最大震级值的1%。

图 4 显示了输入到 ResNet50 的 layer1.0.conv2 的激活的对数比例直方图。由最大值、熵和 99.99% 百分位校准得出的范围用虚线表示。最大值校准代表分布中的最大值，保持全范围，但精度较低。对分布进行裁剪时，在少数离群值上会产生较大的裁剪误差，但在大多数值上只产生较小的舍入误差。熵和百分位校准都会裁剪一些离群值，以提高内部值的分辨率。

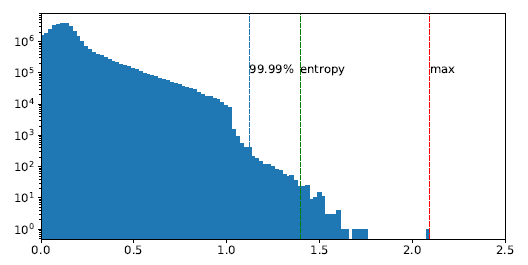
图 4 输入激活的直方图到 ResNet50 的第三层和校准范围

1.3.1 TensorRT 的校准

TensorRT 采用基于实验的迭代搜索阈值。校准是其中的一个主要部分。校准过程如下所示：

  • 首先，需要选择合适的校准数据集（校准集应该具有代表性，多样性，最好是验证集的一个子集），用于执行校准；
  • 在校准数据集上运行 FP32 推理。收集每一层的激活值，并统计其直方图。将直方图分成 2048 个组别（分组是为了遍历|T|  时，减少遍历次数）；
  • 对于不同的阈值|T|  进行遍历，即选取每个组别的中间值进行遍历；
  • 记录使得KLdivergence(P,Q)取得最小值的 |T|，创建校准表 。

TensorRT 校准的伪代码如下所示：

// 首先分成 2048个组，每组包含多个数值（基本都是小数）
Input: FP32 histogram H with 2048 bins: bin[ 0 ], …, bin[ 2047 ] 
  
For i in range( 128 , 2048 ):  // |T|的取值肯定在 第128-2047 组之间，取每组的中点
 reference_distribution_P = [ bin[ 0 ] , ..., bin[ i-1 ] ]  // 选取前 i 组构成 P，i>=128
 outliers_count = sum( bin[ i ] , bin[ i+1 ] , … , bin[ 2047 ] )  // 边界外的组
 reference_distribution_P[ i-1 ] += outliers_count  // 边界外的组加到边界P[i-1]上，没有直接丢掉
 P /= sum(P)  // 归一化
      
    // 将前面的P（包含i个组，i>=128），映射到 0-128 上，映射后的称为Q，Q包含128个组，
    // 一个整数是一组
 candidate_distribution_Q = quantize [ bin[ 0 ], …, bin[ i-1 ] ] into 128 levels
 
 // 这时的 P（包含 i 个组，i>=128）和 Q 向量（包含 128 个组）的大小是不一样的，无法直接计算二者的 KL 散度
 // 因此需要将 Q 扩展为 i 个组，以保证跟 P 大小一样
 expand candidate_distribution_Q to 'i' bins 
 
 Q /= sum(Q)  // 归一化
 
 //计算 P 和 Q 的 KL 散度
 divergence[ i ] = KL_divergence( reference_distribution_P, candidate_distribution_Q)
End For

// 找出 divergence[ i ] 最小的数值，假设 divergence[m] 最小，
// 那么|T|=( m + 0.5 ) * ( width of a bin )
Find index ‘m’ for which divergence[ m ] is minimal

threshold = ( m + 0.5 ) * ( width of a bin )

2. 训练后量化 (Post Training Quantization, PTQ)

在本节中，我们评估各种训练后量化参数选择。量化参数通过处理训练后的模型权重和在校准数据集上运行推理生成的激活进行离线校准，不涉及进一步的训练。

2.1 权重量化

我们首先单独评估权重量化，因为它们的值不依赖于网络输入，并证明最大值校准足以保持 INT8 权重的精度。表 2 比较了 per-channel 和 per-tensor 量化粒度的对量化模型精度的影响。对于某些网络，per-tensor 量化会导致严重的精度损失，如果将 BN 参数折叠到卷积层中，精度损失更为明显，甚至对 EfficientNet 网络来说是灾难性的。BN 折叠是一种常用的加速模型推理的方法，因为它减少了从内存中读取参数和相应计算的时间，并且该操作不改变网络参数的数学计算。由于每个通道都学习 BN 参数，因此它们的折叠会导致通道间的权值分布显著不同。但如表 2 所示，即使在 BN 折叠的情况下，per-channel 量化粒度仍能保持模型精度。表 3 表示了 per-channel 量化粒度，并指出最大值校准足以在将权重量化为 INT8 时保持模型的精度。

表 2 权重的 int8 量化精度: per-tensor 与 per-channel 的对比

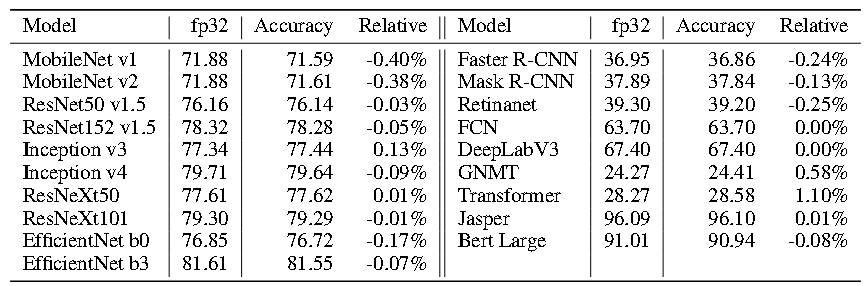
表 3  权重的 int8 量化精度：per-channel 粒度，最大值校准 

2.2 激活量化

表 4 显示了不同校准方法的激活量化结果：最大值、熵和百分位数从 99.9% 到 99.9999%。对于大多数网络，至少有一种激活校准方法使模型达到可接受的精度，但MobileNets、EfficientNets、Transformer 和 BERT 除外，其精度下降大于 1%。最大值校准会导致不同网络的校准效果差距较大，如 Inception v4、EfficientNets 和 Transformer 使用最大值校准时精度损失特别大，可能是由于它们的异常值导致的。99.9% 的百分位校准将大幅度值剪裁得太激进，导致大多数网络的精度显著下降。训练后的最佳量化结果是通过熵、99.99%或99.999%的百分位校准实现的，尽管没有单个校准方法对所有网络都是最好的。

表 4 训练后量化精度。权重使用 per-channel 最大值校准。激活使用列出的校准。每个网络的最佳量化精度以粗体显示

2.3 TensorRT 的 PTQ

图 5 中左边流程图表示 TensorRT PTQ 工作流程，右边框图表示 TensorRT INT8 量化，使用从配置张量动态范围导出的量化缩放因子。

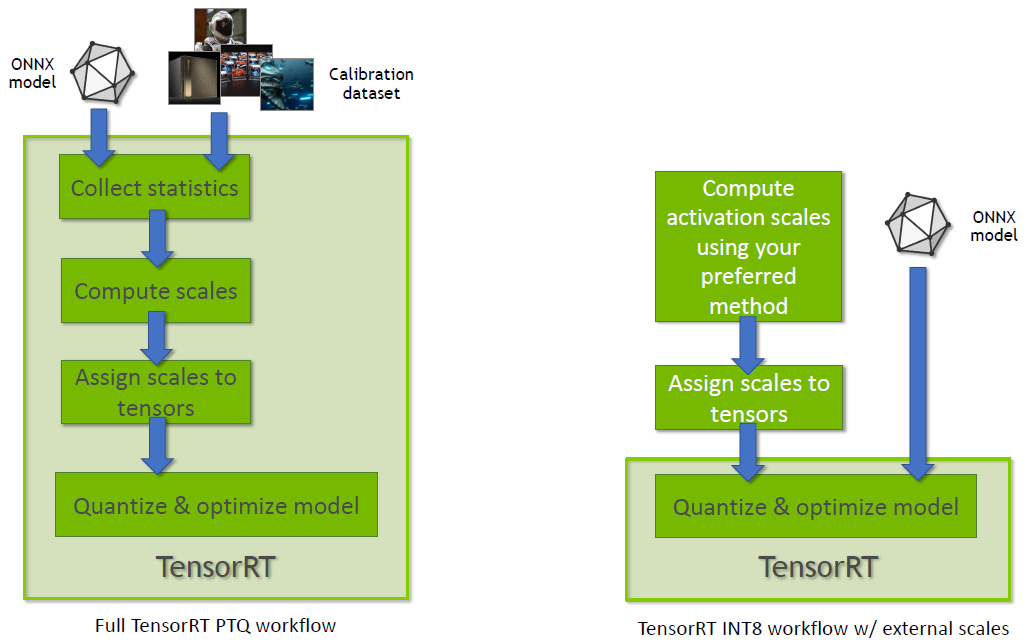
图 5 TensorRT 的两种量化方式 

3. 提高量化精度损失的方法

虽然许多网络在训练后量化后保持一定的精度，但在某些情况下，精度损失很严重。许多方法可用于恢复量化带来的精度损失。最简单的一种是部分量化，即对网络较敏感的层不进行量化。其次， 还可以选择使用量化感知来训练网络。

3.1 部分量化

通常只有几个量化层会导致量化模型的精度损失较大。我们可以通过不量化这些敏感层，将其输入和计算保留为浮点形式，来权衡一些性能以减少精度损失。由于一个层的量化会影响其他层的输入，因此找到要量化的所有层的集合可能需要指数级数量的评估操作。因此，建议使用对网络的每一层进行敏感性分析的方法来推断哪些层导致量化后模型精度的显著下降。

在进行灵敏度分析时，一次量化一个单层，并评估模型精度。我们将量化时导致较低精度的层称为对量化更“敏感”的层。我们按照灵敏度的降序对层进行排序，并跳过最敏感层的量化，直到达到所需的精度。图 6 展示了灵敏度分析和 EfficientNet b0 部分量化的示例。从熵校准开始，一次量化一层并评估其量化后模型精度。图中只展示了模型中 10 个最敏感的层。

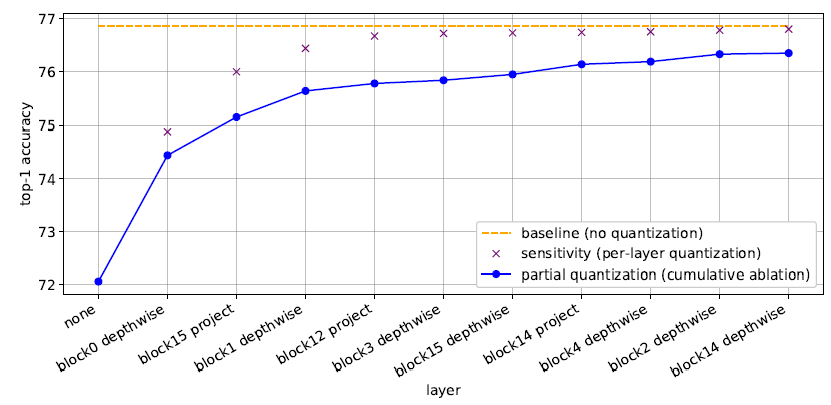
图 6 EfficientNet b0的部分量化，显示10个最敏感层，以提高精度。 

3.2 量化感知训练 (Quantization-Aware Training, QAT)

量化感知训练（QAT）描述了在训练或微调之前将量化操作插入神经网络的方法，以允许网络适应量化权重和激活。将 QAT 应用于微调，有些论文已经证明，从预先训练的网络开始微调可以获得更好的精度，并且可以显著减少网络训练的迭代次数。在整个微调过程中需要保持量化范围固定。实现 QAT 的一种常见方法是将伪量化（也称为模拟量化）操作插入浮点网络，如图 7 所示。公式 (12) 将伪量化定义为产生输入的近似版本的量化和去量化操作，，其中  和x  都是浮点值。

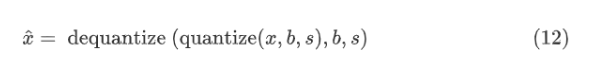
我们在希望量化的操作的输入端添加伪量化操作，以模拟量化的效果。 

图 7 插入伪量化操作 

浮点量化训练面临的一个挑战是量化运算的导数在阶跃边界处未定义，在其他地方为零。需要导数来计算每个训练迭代的反向过程上的损失梯度。QAT 通过使用直通估计器（STE）解决了这一问题，如图 8 所示。如公式 (13) 中所定义，对于可表示范围内的输入 [β,α]，STE 将伪量化函数的导数近似为 1。 

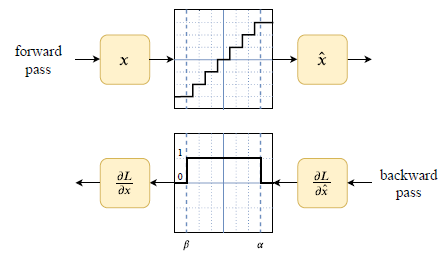
图 8 3-bit 伪量化前向和后向传递 STE 导数逼近

4. 模型量化推荐的流程

根据上述的研究和实验结果，推荐 INT8 量化采用以下方法：

  • 权重
    • 使用 per-channel 粒度的对称量化
    • 使用一个对称整数范围为 [-127,127] 的量化和最大值校准
  • 激活：
    • 使用 per-tensor 粒度的对称量化

推荐采用以下步骤对预先训练的神经网络进行量化：

  • PTQ：量化所有计算密集型层（卷积、线性、矩阵乘法等），运行激活校准，包括最大值、熵和 99.99%、99.999% 百分位数。如果所有校准均未达到所需精度，则继续进行部分量化或 QAT。
  • 部分量化：执行灵敏度分析，以确定最敏感的层，并将其保留为浮点值。如果对计算性能的影响不可接受或无法达到可接受的精度，则使用 QAT。
  • QAT：从最佳校准量化模型开始。使用 QAT 微调原始训练迭代数量的 10% 左右，退火学习率计划从初始训练学习率的 1% 开始。

参考资料

  • 《Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation》
  • Low Precision Inference with TensorRT【https://towardsdatascience.com/low-precision-inference-with-tensorrt-6eb3cda0730b】
  • 利用 NVIDIA TensorRT 量化感知训练实现 INT8 推理的 FP32 精度【https://developer.nvidia.com/zh-cn/blog/chieving-fp32-accuracy-for-int8-inference-using-quantization-aware-training-with-tensorrt/】 
# 人工智能
Logo
兴智开发者社区

更多推荐

cover

深度学习中分类和回归常见损失函数归纳小结

avatar 兴智开发者社区

AI部署：聊一聊深度学习中的模型权重

点击上方“3D视觉工坊”，选择“星标”干货第一时间送达作者丨Oldpan来源丨Oldpan博客编辑丨极市平台导读本文简要介绍了模型权重的统计方法，以及在caffe，pytorch，Ten...

avatar 兴智开发者社区
cover

毕业设计-基于深度学习的时间序列预测方法

avatar 兴智开发者社区