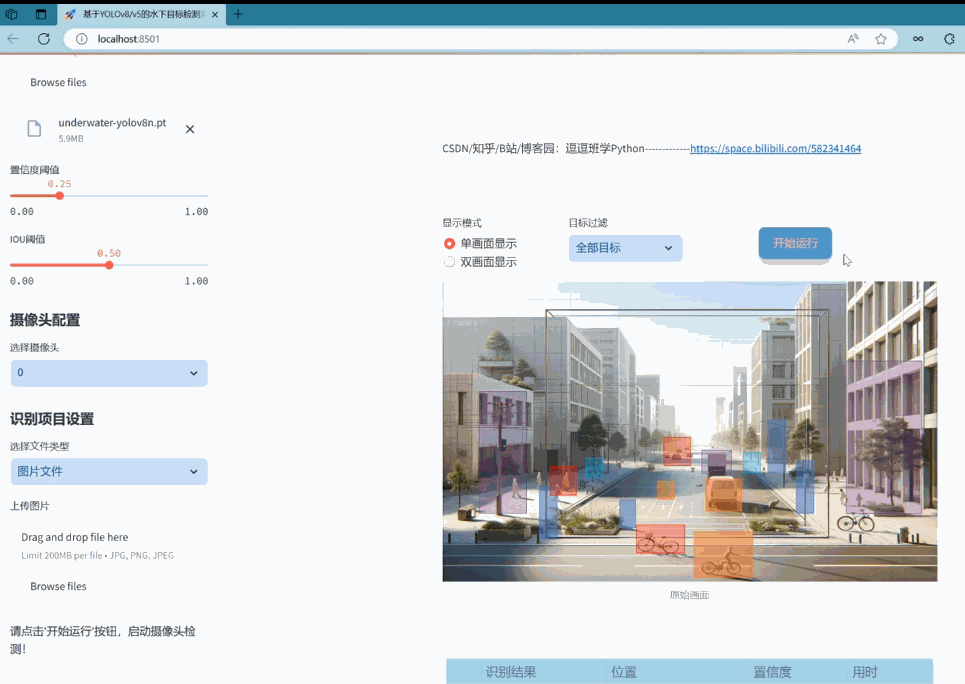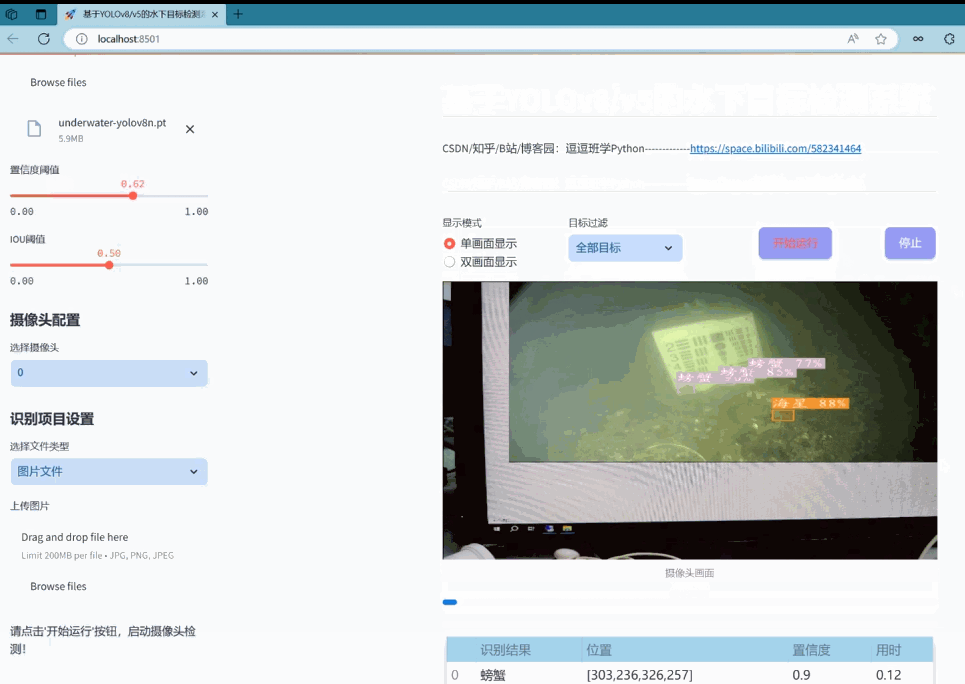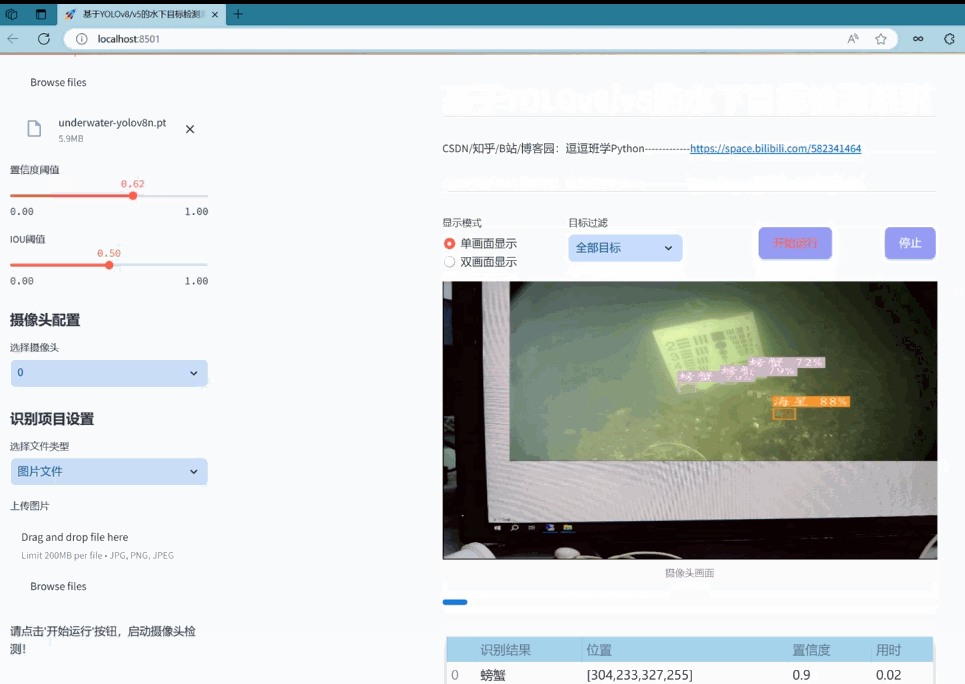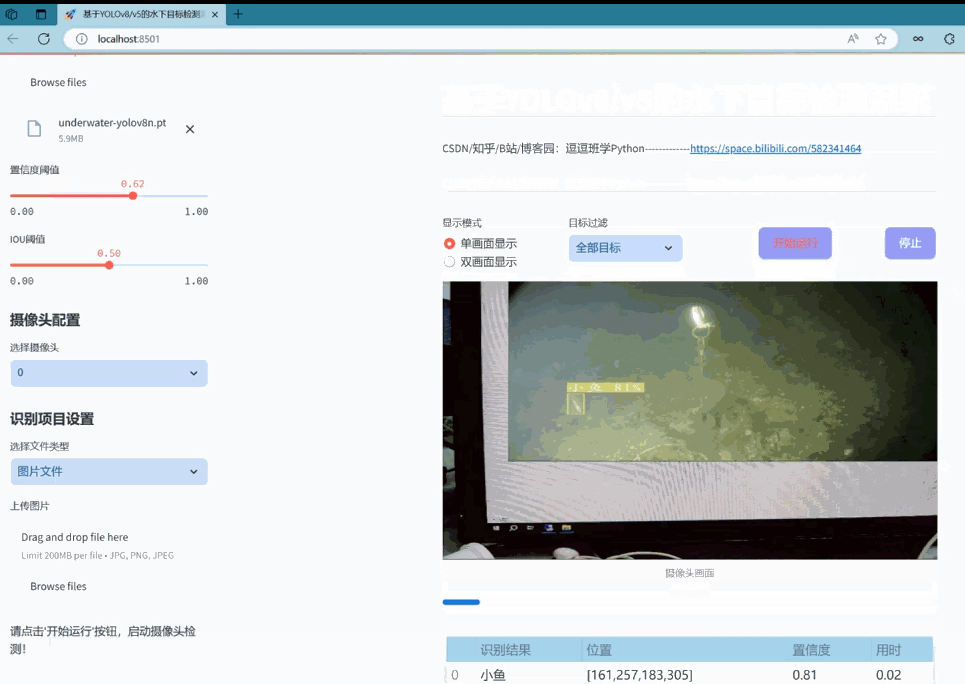
Prophet:一种大规模时间序列预测模型
本文从数学原理出发介绍了facebook开源的Prophet模型,希望能更好的帮助大家理解并使用。参考prophet官方网站:https://facebook.github.io/prophet/
0. 前言
Prophet是由facebook开发的开源时间序列预测程序,擅长处理具有季节性特征大规模商业时间序列数据。本文主要介绍了Prophet模型的设计原理,并与经典的时间序列模型ARIMA进行了对比。
1. Prophet模型原理
Prophet模型把一个时间序列看做由3种主要成分组成:趋势项、季节项、假期项。
![]()
其中趋势项g(t)模拟了时间序列的非周期变化,季节项s(t)模拟了时间序列的周期性变化,假期项h(t)模拟了假期或者其他突发事件的影响,Ɛt为误差项。
1.1 趋势项
趋势项主要说明了数据的变化趋势,Prophet算法中主要运用了两种趋势项模型,饱和式增长模型与分段线性模型。
1.1.1 饱和式增长模型
最基本的饱和式增长模型表示为:

其中,C代表承载能力,k代表增长率,m代表偏移量。该模型并不能完全反应数据特性,要对其进行改造。
首先,模型的承载能力不一定为常数,比如说访问互联网的人口是随时间提高的。因此C可以替换为C(t)。同样的,成长率也不一定为常数,Prophet算法通过设置变点来拟合模型,假设在时间sj,j=1,2,3,...,S设置变点,斜率变化通过δ ϵ ℝS表示,其中δj表示时间sj时刻的变化率。这样在时刻t的变化率可以表示为:k+∑j:t>sjδj,变化率也可以通过α(t)ϵ{0,1}S化简为k+α(t)T δ。
如果对变化率k进行调整,相应的偏移量m也要进行改变,以连接不同段的端点。第j点的偏移量可以表示为:

1.1.2 分段线性模型
对于不体现饱和增长的预测问题,可以考虑使用线性模型进行拟合,
![]()
同样的,为了使分段函数连续,γj=-sjδj
1.2 季节项
商业时间序列通常由于人类行为呈现多周期性,比如5天工作2天休息将会产生以周为周期的季节性效应,寒暑假会产生以年为周期的季节性效应。在Prophet模型中,通过傅里叶级数来拟合周期性效应:

其中P为时间序列周期,为了拟合多周期性数据,P可以取多值,一般为365.25对应年数据,7对应周数据。拟合周期项需要估计2N个参数β=[a1,b1,...,an,bn]T,因此季节项可以表示为:
![]()
例如一个年季节性数据,且N=10,则X(t)可以表示为:

1.3 假期项
节假日或者某些突发事件对商业性的时间序列数据有很大的影响,而且很多事件并不遵循季节性数据的规律,很难用季节性模型建模。Prophet算法中假设假期效应是独立的,对于假期i,Di表示假期所影响的时间段,每个假期项对应参数ki,表示方式与季节项相似:
![]()
其中,
![]()
2. ARIMA模型
Arima模型是由AR、MA与差分法结合而成的一种时间序列预测算法,p阶自回归模型AR(p)表示为:
![]()
这就相当于将预测变量替换为目标变量的历史值的多元回归。
不同于使用预测变量的历史值来进行回归,移动平均模型(moving average model)使用历史预测误差来建立一个类似回归的模型。
![]()
我们将这个模型称之为MA(q)模型,即q阶移动平均模型。
结合MA与AR模型,我们可以得到ARIMA模型:
![]()
上式中y’(t)是差分序列(它可能经过多次差分)。右侧的“预测变量”包括 yt 的延迟值和延迟的误差。我们将这个模型称为ARIMA(p,d,q)模型,其中d为差分次数。
3. 模型对比
ARIMA是自回归预测,它使用滞后值和误差项拟合时间序列,它假设时间序列的过去值与过去误差和未来值之间存在某种因果关系。

图1 arima预测
图1所示为arima预测,一般在短期预测中体现不错的效果,但长期的预测结果接近线性预测。
相反,Prophet不会寻找过去和未来之间的任何此类因果关系,它只是尝试找到适合数据的最佳曲线,使用线性或逻辑曲线以及季节性分量的傅立叶系数。
在ARIMA中,我们可以设置参数自回归分量p、差分次数d和移动平均分量q。为了调整ARIMA模型,我们可以使用自相关函数 (ACF) 和偏自相关函数 (PACF) 图来确定p和q的值。
而在Prophet中,我们可以设置线性或逻辑增长、假期、季节性和变化点。调整变点参数有助于模型捕捉训练数据中的趋势。Prophet提供了接口plot_components来分析数据的组成成份:

图2 prophet分解
图2展示了拟合数据的分解结果。当然,变点设置过多可能会导致模型过拟合,导致模型对未来数据的预测准确性下降。
不同于AIRMA模型要求等间隔采样,Prophet对于异常值、缺失数据和时间序列的剧烈变化具有鲁棒性。
Prophet模型参数可解释性更强,更加灵活,便于分析师对参数进行更改与扩展,比如说如果我们看到数据中存在一些突变值,可以根据需要设置合适的假期项来拟合数据。

图3 prophet预测
图3展示了通过设置合理的假期项来拟合变化复杂的数据。
总结
本文从数学原理出发介绍了facebook开源的Prophet模型,希望能更好的帮助大家理解并使用。具体的程序使用方法可以参考prophet官方网站:https://facebook.github.io/prophet/
更多推荐
 已为社区贡献77条内容
已为社区贡献77条内容








所有评论(0)